A. ARTÍCULOS

 

Casos de localización dinámica exacta bajo la aproximación
semiclásica

 

Exact dynamic localization cases in the semiclassical
approximation

 

 

Edson Anghelo Garcia Foronda ,Diego Sanjinés Castedo ^†, Evaristo Mamani Carlo
^†diegosanjinescastedo@gmail.com
Recibido 20 de agosto de 2021; aceptado 25 de octubre de 2021

 

 

---

Resumen

En este trabajo se aplica los resultados de la aproximación semiclásica y la promediación temporal en una red unidimensional descrita por un Hamiltoniano de enlace fuerte con interacciones de largo alcance a todos los vecinos. La partícula cargada se mueve en esta red en presencia de un campo eléctrico externo homogéneo rápidamente oscilante. Dicha aplicación semiclásica corresponde al teorema de Dignam y de Sterke referido al fenómeno de "localización dinámica exacta" (LDE) y deducido con el formalismo cuántico por esos autores. Para ilustrar la validez de LDE se eligió en este trabajo varios campos eléctricos externos. Los resultados indican que los formalismos semiclásico y cuántico son equivalentes y conducen a las mismas condiciones para LDE.

Descriptores: Método de enlace fuerte - modelo semiclásico - efectos de localización.

---

Código(s) PACS: 31.15.aq, 03.65.Sq, 72.15.Rn

---

Abstract

In this work we apply results from the semiclassical method and time-average techniques to a one-dimensional lattice described by a tight-binding Hamiltonian with long-range interactions to all neighbours. The charged particle moves in the lattice in the presence of an external homogeneous and rapidly oscillating electric field. Such a semiclassical application corresponds to the Dignam and de Sterke theorem referred to as the phenomenon of "exact dynamic localization" (EDL). This theorem has been deduced within the quantum formalism by the authors. To illustrate the validity of EDL, several external electric fields were chosen in this work. The results indicate that the semiclassical and the quantum formalism are equivalent and yield the same conditions for EDL.

Subject headings: Tight-binding method - semiclassical model - localization effects.

---

 

 

1. Introducción

El fenómeno de localización dinámica en redes de enlace fuerte fue descrito por primera vez en el trabajo pionero de Dunlap y Kenkre Dunlap, [1986], donde se definió como localización dinámica el régimen en el que una partícula cargada (por ejemplo, un electrón) oscila en un intervalo acotado de la red por efecto de un campo eléctrico externo periódico en el tiempo. Dicho régimen se deduce de la condición de que el desplazamiento cuadrático medio esté acotado en el estado cuántico del electrón en la red. Dunlap y Kenkre se refirieron a la extensión de su resultado para interacciones de largo alcance a fin de mostrar que en este caso se pierde la condición de localización dinámica para los parámetros correspondientes al caso de interacciones a primeros vecinos; sin embargo, Dunlap y Kenkre estimaron que si las interacciones de largo alcance son pequeñas comparadas con las de primeros vecinos, entonces la condición de localización dinámica podría mantenerse aún de manera aproximada.

En 2002 Dignam y de Sterke Dignam, [2002] mostraron que dicha estimación para una localización dinámica aproximada no puede ser válida aún cuando el elemento de hopping de la interacción a segundos vecinos sea un décimo del elemento correspondiente a primeros vecinos, poniendo en evidencia la necesidad de calcular la forma general que debería tener un campo eléctrico externo para que haya localización dinámica considerando todas las interacciones en una red de enlace fuerte. A este nuevo régimen de localización dinámica se lo denominó "localización dinámica exacta" (LDE). De manera interesante, se encontró que la aplicación del modelo semiclásico y de la promediación temporal para campos rápidamente oscilantes Mamani, [2017,Mamani, [2018,Mamani, [2020] produce en estos casos los mismos resultados de Dunlap y Kenkre, Dignam y de Sterke, y otros, obtenidos con el formalismo cuántico.

Este trabajo se divide en dos partes independientes entre sí: (i) En la Sección 2 se deduce la función hamiltoniana efectiva H_ef bajo la aproximación semiclásica; luego, H_ef se usa en la Sección 3 para justificar por argumentos de plausibilidad la equivalencia entre los esquemas semiclásico y cuántico para describir el régimen de LDE. (ii) En la sección 4 se calcula explícitamente la expresión G₀(n)=0 para la condición de LDE correspondiente a 5 casos de campos eléctricos caracterizados por sus frecuencias e intensidades; los resultados de esta sección no son una consecuencia o aplicación de la Sección 2 pues G₀(n)=0 se puede deducir semiclásicamente o cuánticamente.

 

2. Deducción semiclásica del Hamiltoniano efectivo

En este trabajo se considera el caso de una partícula con masa m y la carga eléctrica del electrón -e, que se propaga por el mecanismo de hopping en una red unidimensional de enlace fuerte con constante de red a y elementos de hopping A_n que determinan la interacción entre la partícula y un ion separados por una distancia na. Sobre la partícula actúa un campo eléctrico externo oscilante f(ωt) con promedio temporal nulo en un periodo. La función hamiltoniana (o Hamiltoniano) que describe este sistema físico es:

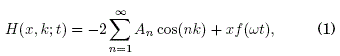
donde se supuso valores unitarios para: a, m, e, y ħ (unidades naturales). La aplicación del método semiclásico consiste de la formulación hamiltoniana expresada por medio de las ecuaciones de Hamilton:

Las ecuaciones de movimiento para las variables dinámicas x y k se obtienen de (2):

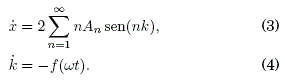
Utilizaremos la transformación canónica k(t) = k’ (t)-g(t) donde g(t) ≡ en (3) y (4) tal que:

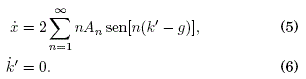
Para este sistema de ecuaciones se propone las soluciones:

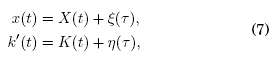
donde X(t) y K(t) son referidas como "coordenadas lentas" y ξ(τ) y η(τ) son referidas como "coordenadas rápidas". Asimismo t y τ ≡ ωt serán referidos como "tiempo rápido" y "tiempo lento", respectivamente. Las derivadas temporales de las variables dinámicas (7) son:

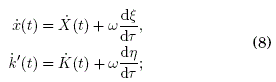
reemplazando (7) y (8) en (5) y (6) se obtiene:

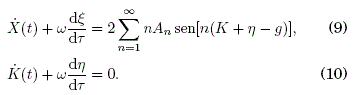
Utilizaremos la definición usual para el promedio temporal: , donde T es el período y (...) es la función a promediar. Suponemos que las coordenadas rápidas tienen un promedio nulo en un período T del campo oscilante f(ωt), mientras que las coordenadas lentas varian muy poco en ese periodo:

Calculando el promedio temporal del sistema de ecuaciones (9) y (10) con las consideraciones ya mostradas, se obtiene:

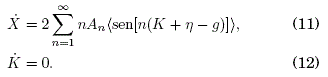
Así, (11) y (12) es el sistema de ecuaciones de movimiento "efectivas" para las coordenadas lentas. Por otro lado, restando (11) de (9) y (12) de (10) se obtiene:

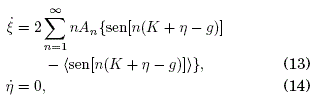
de donde (13) y (14) es el sistema de ecuaciones de movimiento "efectivas" para las coordenadas rápidas. La única solución consistente cuando ξ(t) y η(t) se desarrollan en series hasta ω^-2 es η = 0. Así, las ecuaciones efectivas de movimiento (11) y (12) quedan como:

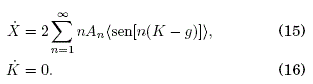
Para encontrar un Hamiltoniano efectivo H(X,K) se integra las ecuaciones (15) y (16) usando:

Ya que la función g(t) es periódica, entonces se puede expresar como:

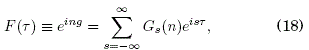
donde:

Así, (18) se escribe como

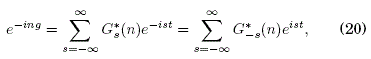
de tal forma que (17) queda en la forma:

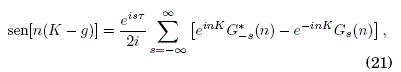
cuyo promedio temporal es:

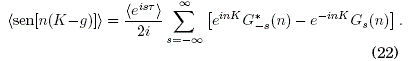
Utilizamos

así que (22) queda como:

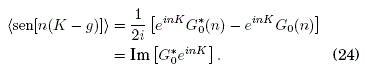
Reemplazando (24) en (15) se obtiene las ecuaciones "efectivas" de movimiento para :

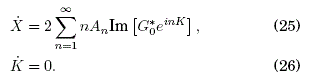
A partir de estas ecuaciones se calculará el Hamiltoniano "efectivo" H(X,K) en el que ya no aparece explícitamente el tiempo t, como consecuencia del proceso de promediación temporal en un período 2π/ω del campo eléctrico externo rápidamente oscilante con promedio temporal nulo.

El Hamiltoniano efectivo H(X,K) ≡ H_ef debe satisfacer las ecuaciones de Hamilton en las variables X y K según:

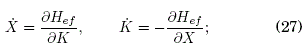
luego, se integra en X :

donde se usó (26). Por otra parte, de y (25) se tiene:

así la expresión para el Hamiltoniano efectivo queda como:

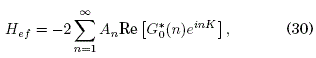
En el trabajo de Mamani et al. Mamani, [2020] se demuestra que si el Hamiltoniano H(x,k;t) en (1) contiene un potencial estático arbitrario V(x), el Hamiltoniano efectivo correspondiente contiene los siguientes términos adicionales:

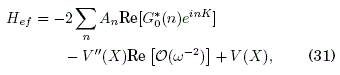
donde

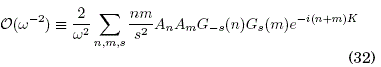
(s ≠ 0) para una red simétrica con A_-n=A_n.

 

3 Condición de LDE

Los términos G₀(n) reparametrizan las interacciones del electrón con todos los iones de la red. Estos términos se pueden manipular controlando la intensidad f₀ y la frecuencia ω del campo eléctrico externo (ingeniería de interacciones); ésto es lo que se hace en la Sección 4 para varios tipos de campos eléctricos. La condición G₀(n)=0 para cualquier valor de n constituye el régimen de localización dinámica exacta (LDE) de acuerdo al siguiente criterio: en el formalismo cuántico el estado del electrón representado por la función de onda Ψ(x,t) debe cumplir la condición Ψ(x, T)=Ψ(x, 0) bajo el efecto de un campo eléctrico períodico f(τ), lo que equivale a un operador de evolución igual a la unidad, = 1, o bien, .

Si en lugar del operador Hamiltoniano dependiente del tiempo , éste se sustituye por un Hamiltoniano efectivo independiente del tiempo , entonces la condición de LDE es = 0, lo que se demuestra por medio de la teoría de Floquet Goldman, [2014]. Aunque dicho Hamiltoniano efectivo se puede calcular cuánticamente, ya sea de manera exacta Kunold, [2019] o de manera aproximada Rahav, [2003], Mamani et al. Mamani, [2020] encontraron que el cálculo semiclásico de la función H_ef = 0 conduce exactamente a la misma condición de LDE reportada por Dignam y de Sterke Dignam, [2002]. La razón de esta coincidencia aún no está dilucidada y se propone en este trabajo como una perspectiva interesante (cf. sección 5), sin embargo, una parte de esa razón puede ser que la deducción de un Hamiltoniano efectivo H_ef (sea cuántico o semiclásico) debe ser consistente con la aproximación de desarrollar en series las soluciones de (13) y (14) para ξ(t) y η(t) hasta O(ω^-2), como condición para la validez de G₀(n) en (19). Dicho de otra manera: G₀(n) = 0 es la condición para LDE válida para cualquier rango de frecuencias, tal como la deducen Dignam y de Sterke Dignam, [2002]; en particular, para altas frecuencias G₀(n) se puede deducir por el método semiclásico tal como se muestra en este trabajo.

La relevancia del resultado semiclásico expresado por el Hamiltoniano efectivo (32) es que éste contiene el término de la energía cinética reparametrizado por el factor G₀(n), más el término V’’(X) O(ω^-2) correspondiente a un potencial estático arbitrario V(X). Cuando G₀(n)=0 y el potencial es lineal, el término de energía cinética se anula y el Hamiltoniano efectivo es H_ef = V(X), lo que sólo se puede interpretar físicamente como un régimen de LDE para las coordenadas "lentas" X(t) y K(t). Esto lo verificamos cuánticamente (durante la elaboración de este artículo) para el Hamiltoniano al que añadió un potencial estático lineal; la integración numérica de la ecuación de Schrödinger se realizó usando una extensión del método pseudoespectral adaptado a un Hamiltoniano de enlace fuerte . En ambos casos, el indicador de LDE es el valor acotado en el tiempo del desplazamiento cuadrático medio ⟨ x²⟩, consistente con la definición original de localización dinámica que hicieran Dunlap y Kenkre Dunlap, [1986].

De hecho, en la definición de LDE, Dignam y de Sterke Dignam, [2002] sólo consideran los campos eléctricos externos puramente AC (sin componente DC) tales que ⟨ f(ωt) ⟩ = 0 en (1). Para incorporar el caso simple de un campo DC tal que la energía potencial sea V(x,t) = xf(ωt) + αx, invocamos la técnica usada por Sandoval-Santana et al. Kunold, [2019] para calcular el Hamiltoniano efectivo exacto correspondiente a la función H(x,k;t) en (1); en este caso el término de energía cinética de se reparametriza por un factor que tiende a J₀(f₀/ω) cuando , con f₀ igual a la amplitud del campo eléctrico f(ωt) en . Por otra parte, el cálculo aproximado de hasta ω^-2 para valores de se puede realizar por el método de Rahav et al. Rahav, [2003], pero el término de energía cinética de es , así que lo que se reparametriza es el potencial efectivo V_ef; un cálculo de para una energía cinética de enlace fuerte de la forma se realizó en Calcina et al. Calcina, [2020] para el caso de un circuito LC de dos mallas con carga discreta. En todos los casos referidos, los cálculo cuánticos de conducen a expresiones analíticas muy complejas que no contienen a las variables dinámicas "lentas" X(t) y K(t). Así, tal parece que la expresión para la función H_ef en (31) deducida en este trabajo por el método semiclásico y las técnicas de promediación temporal usadas por Rahav et al., adaptadas a un Hamiltoniano de enlace fuerte, conducen a una expresión suficientemente simple como para dilucidar el fenómeno de LDE en vista de la cancelación del término de energía cinética en (31) cuando G₀(n) = 0.

A continuación nos referimos a las propiedades del campo eléctrico f(τ) cuando se satisface la condición G₀(n)=0 para LDE: (i) f(τ) no puede ser cero, es decir, f(τ) debe ser discontinua en los valores de τ para los que f(τ) cambia de signo. (ii) El área debajo de la curva entre discontinuidades de f(τ) debe ser un múltiplo entero de . (iii) El promedio temporal de f(τ) en un período T debe ser cero. El cumplimiento de estas condiciones para LDE será referido en adelante como "teorema de Dignam y de Sterke" (TDS). Para los campos eléctricos relativamente simples caracterizados sólo por los parámetros físicos f₀ y ω, se podría tratar de expresar la condición G₀(n)=0 en como un problema inverso para despejar los valores de esos parámetros, pero éste puede ser un problema muy complicado. En la siguiente sección se estudiará los casos específicos de 5 campos eléctricos a fin de determinar los valores de f₀ y ω para los que se verifica la condición de LDE.

 

4. Casos de campos eléctricos

4.1 Onda rectangular

Consideremos el siguiente modelo para el campo eléctrico f(ωt ≡ τ) del tipo onda rectangular:

donde f₀ es la intensidad del campo. En este caso la expresión para G₀(n) , con n entero, es:

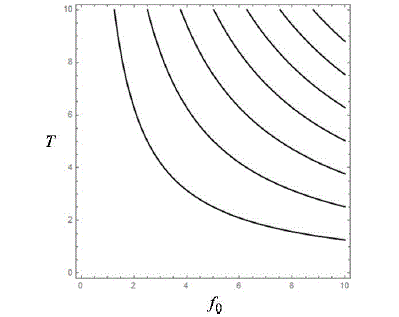
Las soluciones de G₀(n) = 0 corresponden a valores enteros positivos pares de f₀/ω. En la Figura 1 se muestra los valores de f₀ y el período T para los cuales G₀(n) = 0. Por lo tanto, el campo eléctrico tipo onda rectangular produce LDE, de acuerdo al TDS.

Figure 1: Valores de la intensidad f₀ y del período T=2π/ω de la onda rectangular para los que se
cumple G₀(n)=0. Se muestra las curvas que corresponden a valores enteros positivos pares
de f₀/ω (en orden creciente de izquierda a derecha).

4.2 Onda triangular simétrica

A continuación consideremos el caso del campo eléctrico tipo onda triangular simétrica definido por:

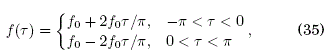
donde f₀ es la intensidad del campo. La evaluación de G₀(n) en (19) es:

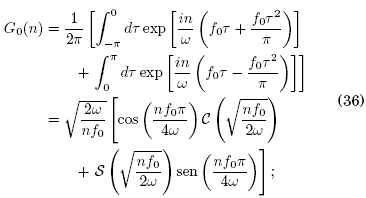
son las integrales de Fresnel.

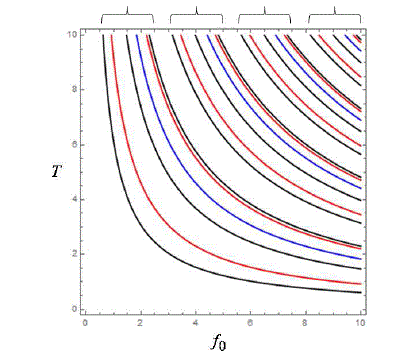
Para que un campo produzca LDE, las soluciones de G₀(n)=0 deben ser iguales para todo valor de n. En la Figura 2 se muestra los valores de la intensidad f₀ y el período T para n=1,2,3. Podemos ver que dichos valores son diferentes para cada n. Por lo tanto, el campo eléctrico tipo onda triangular simétrica no produce LDE, de acuerdo al TDS.

Figure 2: Valores de la intensidad f₀ y del período T de la onda triangular simétrica para los que se cumple G₀(n)=0.
La posición de cada línea (de izquierda a derecha) en cada grupo indicado por las llaves corresponde a los sgtes.
valores de n: 4ta. línea (n=1), 2da. y 5ta. líneas (n=2), 1ra., 3ra. y 6ta. líneas (n=3).

4.3 Onda diente de sierra

A continuación consideremos el caso del campo eléctrico tipo onda diente de sierra definido por:

(este campo tiene simetría temporal impar respecto a τ = 0). La evaluación de G₀(n) en (19) es:

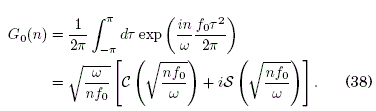
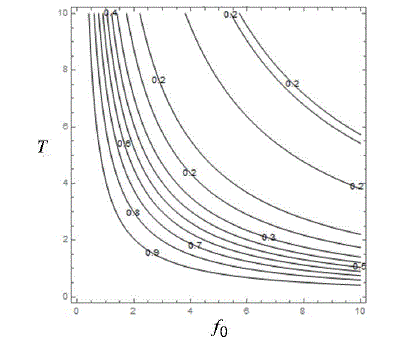
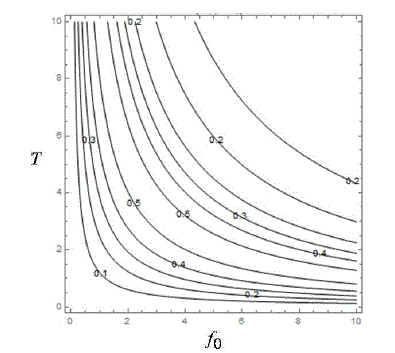
En las Figuras 3 y 4 se muestra los gráficos de Re &[G₀(n)=0] y Im[G₀(n)=0] respectivamente (para n=1), en función de los parámetros físicos f₀ y T. Como se puede ver, la tendencia de estas figuras sugiere que no existen combinaciones de dichos parámetros para los que se cumpla G₀(1)=0 . Por lo tanto, el campo eléctrico tipo onda diente se sierra no produce LDE, de nuevo de acuerdo al TDS.

Figure 3: Valores de las curvas de nivel de Re[G₀(1)] para la onda diente de sierra, en función
de sus parámetros de intensidad f₀ y período T.

 

Figure 4: Valores de las curvas de nivel de Im[G₀(1)]=0 para la onda diente de sierra, en
función de sus parámetros de intensidad f₀ y período T.

 

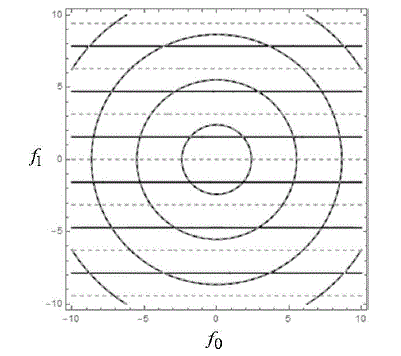
Figure 5: Valores de los parámetros f₀ y f₁ en de la onda cosenoidal desplazada para los que se
cumple: Re[G₀(1)]=0 (intersecciones de las lineas horizontales sólidas con las circunferencias) y Im[G₀(1)]=0
(intesecciones de las lineas horizontales segmentadas con las circunferencias).

4.4 Onda cosenoidal desplazada

A continuación consideremos el caso del campo eléctrico tipo onda cos(τ+ Φ) expresado como:

(este campo no tiene simetría temporal definida respecto a τ = 0). La evaluación de G₀(n) en (19) es:

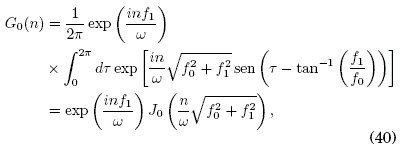
donde J₀ es la función de Bessel de primera clase y de orden entero cero. En este caso se tuvo que elegir un valor unitario de ω en unidades de f₁ a fin de obtener el resultado análitico de (8), de lo contrario dicha expresión para G₀(n) sólo se hubiera podido evaluar numéricamente. De esta forma, las intensidades f₀ y f₁ son los nuevos parámetros físicos de control. En la Figura 5 se muestran los valores de los parámetros f₀ y f₁ en (40) para los que se cumple: Re[G₀(1)]=0 (intesecciones de las lineas horizontales sólidas con las circunferencias) y Im[G₀(1)]=0 (intesecciones de las lineas horizontales segmentadas con las circunferencias). Como se ve, no existen combinaciones posibles de f₀ y f₁ para los que G₀(1)=0, de donde se concluye que para este campo eléctrico no se obtiene LDE, lo que está de acuerdo al TDS, ya que este campo no contiene discontinuidades.

4.5 Serie alternada de deltas de Dirac

A continuación consideremos el campo eléctrico tipo serie alternada de deltas de Dirac dado por la deltoide expresada como:

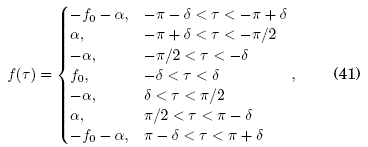
donde los parámetros de intensidad f₀ y ancho δ tenderán a infinito y a cero respectivamente, para obtener la serie de deltas de Dirac. El desplazamiento dado por el parámetro α ≠ 0 tiene como propósito que f(τ) no sea cero, permitiendo de este modo la aplicación del TDS. Además, la forma particular de haber definido dicho desplazamiento en (41) se justifica a fin de que el promedio temporal de f(τ) en un período sea cero: (f(τ) )_T = 0, tal como lo requiere dicho teorema. Para este caso, la evaluación de G₀(n) en (19) es:

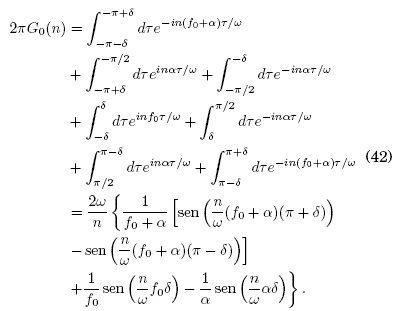
Llevando f₀ y δ a sus respectivos límites para formar la delta de Dirac, se obtiene G₀(n)=0 para todos los valores de n y de ω (independientemente del valor de α ≠ 0), de donde se concluye que la serie alternada de deltas de Dirac siempre produce LDE. Este resultado es muy interesante pues estrictamente la serie de deltas de Dirac no podría ser considerada en el trabajo de Dignam y de Sterke debido a que no satisface el TDS, a menos que sea modelada por la deltoide f(τ) en (41).

 

5. Conclusiones y perspectivas

En este trabajo se calculó los parámetros físicos de los campos eléctricos externos que inducen el régimen de localización dinámica exacta (LDE) en una partícula cargada propágandose en una red unidimensional de enlace fuerte. La ecuación G₀(n)=0 en (19) que permite deducir los valores de dichos parámetros se obtuvo a partir de las ecuaciones semiclásicas de movimiento (2). Por simplicidad, en este trabajo se muestra la deducción que corresponde al caso de un campo eléctrico AC en (1) con promedio temporal nulo (en un período), < f(ωt) > =0, y potencial estático V(x) asimismo nulo. La generalización a los casos ⟨ f(ωt) ⟩ ≠ 0 y V(x) arbitario se indica en las ecs. (31) y (32) aplicando las mismas técnicas de la Sección 2; el detalle específico de este cáculo se publicará próximamente.

El concepto de LDE se definió en el trabajo de Dignam y de Sterke Dignam, [2002] para un operador Hamiltoniano dependiente del tiempo, mientras que en la formulación semiclásica de este trabajo se deduce una función hamiltoniana efectiva independiente del tiempo cuyo valor debe ser cero a fin de inducir el régimen de LDE. Esta condición es la que permite obtener una expresión para G₀(n)=0 y que resulta ser la misma que se obtiene en el formalismo cuántico del referido trabajo. Esta coincidencia seguramente se puede deducir de relaciones conceptuales más profundas asociadas al teorema de aceleración aplicado a redes de enlace fuerte (ver, por ejemplo, el texto de Kittel, [1987]). Éste es un tema que se propone como una perspectiva interesante de investigación para ser explorada en otro trabajo más amplio.

Específicamente, en este trabajo se dedujeron los parámetros físicos ya referidos correspondientes a 5 campos eléctricos. Para algunos campos la condición G₀(n)=0 conduce a expresiones analíticas de las que se deducen los valores de esos parámetros y en otros casos esos valores se deben calcular numéricamente. De manera interesante, en este trabajo se encontró que el campo eléctrico del tipo serie alternada de deltas de Dirac siempre conduce a LDE, independientemente de su intensidad y período, caso que no puede tratarse bajo el formalismo cuántico de Dignam y de Sterke Dignam, [2002]. Sin embargo, el único ejemplo novedoso expuesto por esos autores coincide en sus aspectos esenciales con el resultado de este trabajo para la referida serie alternada de deltas, de lo que se puede concluir que en el ejemplo de Dignam y de Sterke sólo es relevante la naturaleza singular (valores instantáneos infinitos) del campo eléctrico externo y no así los detalles de su forma particular para valores finitos.

Conflicto de intereses Los autores declaran que no hay conflicto de intereses con respecto a la publicación de éste documento.

 

References

[Calcina 2020]

    Calcina-Nogales M., Sanjinés D. & Mamani E. 2020, (preprint).         [ Links ]

[Dunlap 1986]

    Dunlap D. H. & Kenkre V. M. 1986, Phys. Rev. B 34, 3625-3633.         [ Links ]

[Dignam 2002]

    Dignam M. M. y Martijn de Sterke C. 2002, Phys. Rev. Lett. 88, 046806.         [ Links ]

[Goldman 2014]

    Goldman N. & Dalibard J. 2014 Phys. Rev. X 68, 031027.         [ Links ]

[Kittel 1987]

    Kittel C., Quantum Theory of Solids (John Wiley and Sons, New York).         [ Links ]

[Mamani 2017]

    Mamani E., Calcina-Nogales M. & Sanjinés D. 2017, International Journal of Modern Physics B 31, 1750116.         [ Links ]

[Mamani 2018]

    Mamani E., Calcina-Nogales M. & Sanjinés D. 2018, Revista Mexicana de Física 64, 456-463.         [ Links ]

[Mamani 2020]

    Mamani E., Sanjinés D. & Calcina-Nogales M. 2020, (preprint).         [ Links ]

[Rahav 2003]

    Rahav S., Gilary I. & Fishman S. 2003, Phys. Rev. A 68, 013820.         [ Links ]

[Kunold 2019]

    Sandoval-Santana J. C., Ibarra-Sierra V. G., Cardoso J. L., Kunold A., Román-Taboada P. & Naumis G. 2019, Ann. Phys., 531, 1900035.         [ Links ]

[Sanjines 1999]

    Sanjines D. & Gallinar J.-P. 1999, J. Phys.:Cond. Matter 11, 3729-3742.         [ Links ]