D. ENSEÑANZA DE LA FÍSICA

 

El telescopio: una primera ventana al universo

 

The telescope: a first window to universe

 

 

Gabriela Conde-Saavedra^†
Instituto de Investigaciones Físicas, Universidad Mayor de San Andres
c. 27 Cota-Cota, Campus Universitario, Casilla de Correos 8635
La Paz - Bolivia
^†gabrielacondesaavedra@gmail.com

 

 

---

RESUMEN

El telescopio es un instrumento que permite observar objetos muy lejanos. Si queremos comprender su funcionamiento necesitamos algunos conceptos basicos de óptica, pero antes vamos a clasificar los principales tipos de telescopios. Posteriormente, describiremos los conceptos de óptica más relevantes, presentaremos algunos ejemplos y dejaremos algunos problemas propuestos.

Código(s) PACS: 95.55.Cs — 42.00.00 — 01.65.+g

Descriptores: Telescopios — óptica — historia de la ciencia

---

ABSTRACT

The telescope is an instrument that allows for the observation of very far objects. To understand how they work we need to classify the main types of telescopes and to understand some basic optical concepts. Finally, we describe the most relevant optical principles with examples and answer some frequently asked questions.

Subject headings: Telescopes — optics — history of science

---

 

 

1. INTRODUCCIÓN

Alrededor de 1608, Hans Lippershey, un inventor y fabricante de lentes holandes, construye lo que ahora conocemos como catalejo. Un instrumento compuesto por dos lentes, uno fijo y otro movil, situados en un pequeno tubo que permiten observar objetos lejanos. Cuando este instrumento llega a manos de Galileo Galilei en 1609, el decide modificarlo mejorando el aumento y así observar el cielo. Con las observaciones de la Luna, de Jupiter, del Sol y de las estrellas, obtiene las pruebas irrefutables a favor de la teoría Copernicana, teoria que planteaba que el Sol era el centro del Universo, y no la Tierra como sugeria Aristóteles y defendía ciegamente la Iglesia.

La evolución del telescopio es tan fascinante como la vida misma de Galileo Galilei. Desde entonces, este instrumento nos ha revelado las imagenes más sorprendentes del Universo.

 

2. TIPOS DE TELESCOPIO

Existen tres tipos principales de telescopios: el refractor (galileano), el reflector (newtoniano) y el catadioptrico. El telescopio Galileano utiliza lentes, el telescopio Newtoniano se compone de espejos y el catadioptrico combina espejos y lentes. A continuación describiremos un poco más cada uno de estos telescopios.

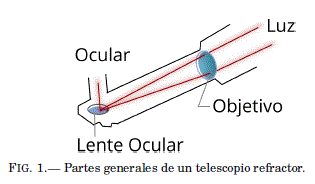
2.1. El Refractor

Denominado tambien como telescopio Galileano, es un sistema optico compuesto por dos lentes situados en los extremos de un tubo. En el extremo del frente esta una lente convergente llamada objetivo, por la cual ingresa la luz del objeto celeste y se refracta hasta concentrarse en el foco, donde se forma la imagen. Situado en el extremo opuesto del tubo, se coloca una lente divergente, denominada ocular, a traves del cual los rayos que pasan por él incrementan en angulo. Esto implica que el tamaño angular aparente es incrementado y la imagen del objeto es ampliada.

Desde 1600 hasta 1900 se ha utilizado el telescopio refractor para observar el cielo. Las variaciones en su diseno están caracterizadas por el diámetro del objetivo; a mayor apertura, mayor luz captada y esto permite tener mayor aumento, o una distancia focal corta. Es decir, los telescopios refractores de poca abertura, necesitaran tubos largos y los de gran abertura necesitaran tubos cortos. Existe aquí un juego de costo y calidad en la imagen a observar. Fabricar lentes de grandes diametros es costoso ya que estos lentes no deben tener ninguna irregularidad y por otro lado, construir tubos largos es tambien una tarea complicada.

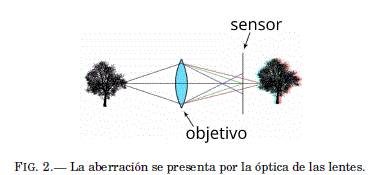
Otro detalle importante en la observación a través de un telescopio refractor es el problema de la aberración cromática, causada por los rayos periféricos que ingresan por el objetivo y no llegan a concentrarse en el punto focal. Los rayos que llegan al foco son mayormente del centro del objeto, de modo que cuando observamos a traves de un telescopio refractor, veremos que el borde del objeto no es nítido y presenta colores.

Los telescopios Galileanos son mas apropiados para observación terrestre, o de la Luna, los planetas y algunas estrellas binarias. Son duraderos y casi no necesitan de mantenimiento porque las lentes estan protegidas por el tubo.

2.2. El Reflector

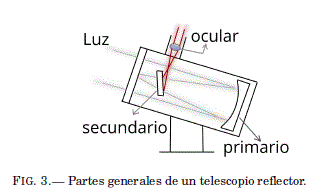
Conocido tambien como telescopio Newtoniano, fue construido en 1668 por Isaac Newton. Esta compuesto por un espejo primario (concavo) en el que la luz se refleja hacia el otro extremo del tubo, donde se situa un espejo secundario (plano) que direcciona los rayos hacia un lado del tubo, lugar del ocular. Como el objetivo (espejo primario) del reflector es parabolico, el problema de la aberración cromática se soluciona puesto que todos los rayos de luz se concentran en un solo punto del plano focal.

Isaac Newton sospechaba que la luz blanca se componía de un espectro de colores y que la aberración cromática era justamente resultado de esta sospecha. Las lentes de un telescopio refractor se comportan como un prisma que refracta la luz en diferentes longitudes de onda (colores). Así que, si en vez de utilizar lentes se utiliza un espejo curvo, esta aberración cromática desaparece. Es de esta manera que Newton comprueba satisfactoriamente su idea. El telescopio Newtoniano le permitio observar las lunas Galileanas de Jupiter y la fase creciente de Venus.

Ademas de solucionar el problema de la aberración cromatica, el telescopio Newtoniano es mucho más compacto y menos costoso. Se puede tener a la vez una abertura amplia y un tubo corto. Sin embargo, se presenta otro tipo de aberración que produce una imagen alargada, como un cometa, en los bordes del campo de vision. Además, debido al transporte del telescopio, los espejos puede quedar desalineados, por lo que conviene realizar una colimación cada vez que se lo monta. Por ultimo, la posición del ocular puede no situarse en lugares comodos para el observador, esto implicaría la necesidad de una escalera para observar a traves del ocular.

Los telescopios Newtonianos son mas apropiados para observar objetos de poca intensidad como galaxias, nebulosas y cumulos estelares. Son instrumentos de mayor cuidado y mantenimiento.

2.3. El Catadióptrico

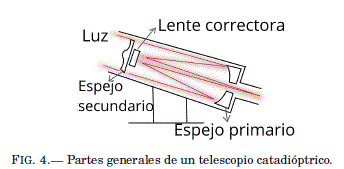
En un sistema catadioptrico, reflexión y refracción se combinan para formar una imagen con menos aberraciones. La luz ingresa a traves de una lente correctora y se dirige hacia un espejo primario esferico, donde se refleja y llega a un espejo secundario. Por ultimo, la luz o la imagen se refleja en el secundario y sale por el ocular, situado en la parte trasera del telescopio.

La ventaja de un catadioptrico es que permite observar planetas, así como objetos de cielo profundo e incluso realizar observación terrestre. A pesar de que su costo es mayor, el catadioptrico es más popular puesto que ademas de las ventajas en la observación, es un instrumento mucho mas compacto y duradero.

 

3. ÓPTICA

La óptica es una rama de la física que estudia el comportamiento de la luz, sus características y manifestaciones como la reflexion, refracción, difracción, interferencias, la formación de imágenes y la interacción entre luz y materia. Al describir los telescopios hemos hablado de lentes concavos, aumento, plano focal o foco, espejos, reflexion y refracción. Vamos a describir brevemente cada uno de estos conceptos para entender mejor el funcionamiento del telescopio.

3.1. Manifestaciones

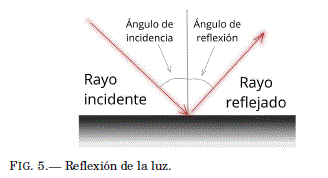
Reflexión. Cuando la luz llega a una superficie de un material, parte de la luz incidente se refleja y la otra parte se absorbe en el material. La Ley de Reflexion indica que el ángulo de incidencia de un rayo de luz es igual al angulo de reflexión. Usualmente, el angulo se mide respecto a una línea perpendicular a la superficie reflectora; como se observa en la figura 5. Si la superficie donde se refleja es opaca y esta muy bien pulida, existe solamente reflexión y no absorción . Esta superficie es un espejo.

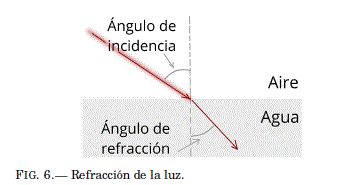
Refracción. Cuando un haz de luz incide sobre un material, puede pasar de un medio a otro desviandose con un ángulo dependiente de las propiedades de los medios y del angulo incidente.

Se experimenta la refracción cuando observamos el lapiz torcido dentro de un vaso con agua, o cuando parece que un pez esta más cerca de la superficie del agua e incluso, algo aumentado de tamaño.

Vamos a definir el índice de refracción de un medio como la razon entre la velocidad de la luz en el vacío y la velocidad de la luz en el medio:

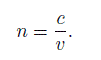
La Ley de Snell para la refracción entre dos medios en general tiene la siguiente expresion:

donde los angulos siempre se miden respecto a la vertical. El índice de refracción para el vacío es 1.

Los prismas o lentes refractan los rayos de luz que les llegan. Pueden tener diversas formas y hacer que los haces refractados converjan o diverjan en el nuevo medio.

3.2. Espejos

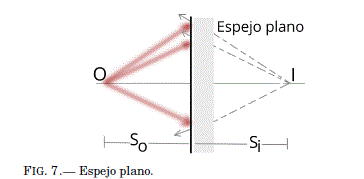
Espejo plano. Si extendemos los rayos reflejados hacia la parte posterior del espejo, todos coincidiran en un punto "detras del espejo" donde se formará la imagen I. La distancia(S_i) de la imagen I es la misma distancia(S_o) del objeto O, que esta delante del espejo.

Por la experiencia cotidiana sabemos que al mirarnos al espejo, nuestra imagen no se modifica en cuanto a altura. Esto quiere decir que el aumento del objeto es 1. Tenemos la ecuación general:

Pero, lo que sí observamos es que si levantamos nuestro brazo derecho, la imagen levanta su brazo izquierdo, asi que para espejos planos decimos que:

•  la distancia de la imagen detras del espejo es igual a la distancia del objeto delante del espejo.

•  la imagen se forma detras del espejo, es virtual y no se invierte.

•  la imagen no se magnifica.

•  la imagen se invierte de atras hacia adelante.

Ejemplo 1. Se coloca un foco a 25 cm de un espejo plano. ¿A que distancia del espejo se encuentra la imagen?

Solución. Como la condición es s_o = -s_i, la imagen se situa a s_i = -25 cm. Interpretando, la imagen esta detras del espejo por el signo negativo y a la misma distancia del objeto.

Magia en la clase 1. ¿Puede el profesor levitar? ¿Que está sucediendo? ¿Puede Ud. mejorar estos trucos de "magia" y sorprender a sus estudiantes? Consiga un espejo y colóquese como en las imágenes, dara la impresión de estar flotando.

Magia en la clase 2. ¿De donde vienen las imagenes? Junte dos espejos planos de modo que formen un angulo recto y observe su reflejo...o reflejos?

Cuando un objeto se coloca frente a dos espejos perpendiculares entre sí, se forman tres imagenes. Como son dos espejos, se forman dos imagenes (I₁ , I₂) detras de cada uno, la tercera imagen I₃ corresponde a la imagen I₁.

Los espejos pueden ser curvos tambien. Estos espejos se caracterizan por tener un radio de curvatura R y un centro de curvatura situado en un punto sobre el eje principal que pasa perpendicular al espejo. En un espejo curvo, los tamaños y las distancias entre objeto e imagen ya no son iguales como en el espejo plano.

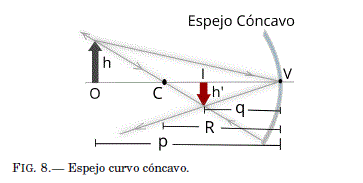
Espejo curvo cóncavo. Es un espejo donde la luz se refleja en la superficie concava interior. Cuando un objeto O de altura h esta fuera del centro de curvatura C, la imagen I formada por el espejo concavo se ubica sobre el eje principal a distancia q del vertice V del espejo. Esta imagen puede tener una altura diferente h'. La magnificación está definida por la misma ecuación que presentamos en el espejo plano:

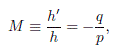
donde p es la distancia entre el vertice del espejo y la posición del objeto.

Si conocemos el radio de curvatura del espejo, podemos determinar el lugar donde se formara la imagen mediante la ecuación del espejo:

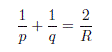
Los rayos luminosos provenientes de un objeto distante que se reflejan en un espejo concavo pasan por el punto focal F. La longitud focal de un espejo esta dada por: ƒ = R/2.

Así, la ecuación del espejo puede expresarse en función de la longitud focal:

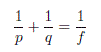
Ejemplo 2. Un objeto se coloca a 40 cm de un espejo esferico cóncavo de 30 cm de radio. ¿A qué distancia del espejo se forma la imagen?

Solución. Como datos tenemos p = 40 cm, R = 30 cm y queremos hallar q. De la ecuación del espejo, resolvemos para q.

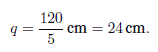
Interpretando, el signo positivo indica que la imagen es real, es decir esta frente al espejo. Podemos obtener la magnificación mediante la ecuación: M = -q/p. Entonces, M = -0.6. El signo negativo indica que la imagen esta invertida y el valor implica que la imagen se reduce al 60%.

Problema 1. Un objeto esta a 25 cm de un espejo concavo. La imagen real está a 50 cm. ¿Que radio tiene el espejo? Resp. 33.3 cm.

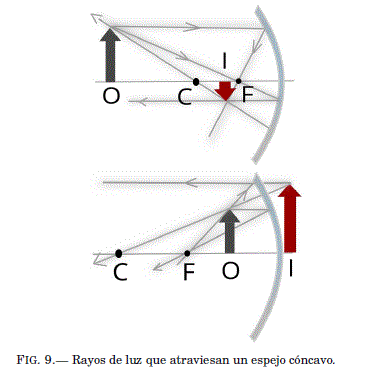
Problema 2. Suponga que un espejo concavo tiene una longitud focal de 10.0 cm. Encuentre la ubicación de la imagen para distancias al objeto de (a) 25.0 cm, (b) 10.0 cm y (c) 5.00 cm. Interprete el resultado calculando ademas el aumento. Resp. (a) 16.7 cm, (b) ∞, (c)  -10.0 cm.

Espejo curvo convexo. Es un espejo en el que la luz se refleja sobre la superficie convexa exterior. Tambien se conoce como espejo divergente puesto que los rayos que inciden sobre el divergen después de la incidencia. Las ecuaciones son las mismas para el aumento, la longitud focal y la ecuación del espejo. La convención de signos es: negativa si la imagen esta detrás del espejo, positiva si está delante, positivo el aumento para una imagen de pie y negativo el aumento para una imagen invertida. Ademas, la longitud focal de un espejo convexo es negativa.

Ejemplo 3. Un objeto se coloca a 35 cm de un espejo esferico convexo de 20 cm de radio. ¿A que distancia se forma la imagen?

Solución. Si p = 35 cm, R=-20cm, entonces resolvemos para q. Utilizando la ecuación del espejo, resolvemos para:

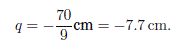
Interpretando, la imagen formada es virtual porque esta detrás del espejo y el aumento M = -q/p = 0.22 nos dice que la imagen esta de pie y se reduce al 22%.

Problema 3. Un objeto de 3.00 cm de altura se situa a 20.0 cm de un espejo convexo que tiene una longitud focal de 8.00 cm. Encuentre (a) la posición de la imagen final, y (b) el aumento. Resp. -5.71 cm, 0.286.

3.3. Lentes

Una lente se puede considerar como un conjunto de bloques y prismas que refractan los rayos de luz. Claro que al fabricar una lente, no se utilizan diferentes piezas, sino que piezas de vidrio son talladas, generalmente de forma esférica.

Como una lente tiene dos superficies, tiene dos centros de curvatura, dos distancias focales o focos y un eje principal.

Se consideran dos tipos de lentes:

Lentes convergentes. Tienen dos superficies convexas y cuando los rayos paralelos de luz inciden sobre una lente convergente, los rayos refractados coinciden en un punto, denominado el punto focal o foco. Un telescopio refractor contiene estas lentes convergentes o biconvexas. Otro ejemplo es la lupa, con la que la imagen es aumentada, esta derecha y se la ve mas lejos que el objeto mismo, cuando éste esta dentro del foco.

En cambio, si el objeto esta muy lejos, mediante una lente convergente se observa una imagen invertida. Esto ultimo puede aprovecharse para proyectar películas y transparencias en una pantalla o para observar objetos celestes mediante el telescopio.

Lentes divergentes. Tienen dos superficies concavas y cuando los rayos inciden sobre ella, se refractan sin coincidir en un punto, es decir, divergen. Una lente divergente forma una imagen virtual, derecha y mas pequeña que el objeto real, por ejemplo las lentes "buscadoras" de las camaras fotograficas. Otra aplicación se encuentra en las lentes para corregir la miopia. Las personas con miopía ven imagenes borrosas si los objetos están lejanos porque la imagen se forma antes de la retina, esto es corregido con las lentes divergentes.

Para lentes delgadas, la ecuación que se utiliza en lentes es la misma para espejos, de igual forma con el aumento. La convención de signos es que la distancia focal es negativa si se trata de una lente divergente y positiva para una lente convergente. La posición del objeto y de la imagen siguen la misma convención que de los espejos.

Ejemplo 4. Una lente convergente de 10.0 cm de longitud focal forma una imagen de un objeto situado a (a) 30.0 cm, (b) 20.0 cm, y (c) 5.00 cm de la lente. Encuentre la distancia a la imagen y su aumento.

Solución. Datos son: la distancia focal ƒ = 10.0 cm, p = 30.0 cm, p = 20.0 cm, y p = 5.00 cm. Queremos calcular la posición de la imagen q y el aumento M. Aplicamos las ecuaciones de lentes delgadas y del aumento:

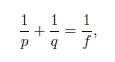
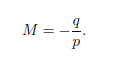
(a) Resolviendo para q obtenemos: q = 15.0 cm. Su aumento es de M = -0.5. Interpretamos que la imagen se forma delante de la lente, es real, esta invertida y se reduce a la mitad.

(b)  Obtenemos: q = ∞ y un aumento de M = ∞. Interpretamos que como el objeto se situa en el foco de la lente convergente, entonces la imagen se forma en el infinito. No se ve.

(c)  Obtenemos la distancia: q = -10.0 cm y un aumento de M = 2.0. El signo negativo de q indica que la imagen es virtual y por el aumento decimos que incrementa su tamaño al doble, además el signo del aumento nos indica que la imagen esta de pie.

Ejemplo 5. Una lente divergente tiene una longitud focal de —20.0 cm. Un objeto de 2.00 cm de altura se pone a 30.0 cm frente al lente. Localice la posición de la imagen, el aumento y la altura de la imagen.

Solución. Nuestros datos son: ƒ = -20.0 cm, h = 2.0 cm y p = 30.0 cm . Queremos calcular q, M y h'. Por la ecuación de lentes delgadas resolvemos para la posición de la imagen, obteniendo q = -12.0 cm, con un aumento de M = 0.4 y la altura h' = 0.8 cm. Interpretando los resultados, decimos que la imagen es virtual por q < 0, esta invertida por M < 0 y de 2.0 cm de altura se reduce a 0.8 cm.

Problema 4. Una lente convergente tiene una distancia focal de 20 cm. Se coloca un objeto a 11 cm, a 30 cm, y a unos 60 cm de la lente. ¿Que amplificación lateral tiene la imagen, en cada caso? Interprete los resultados. Resp. 2.2, -2, -0.5.

Problema 5. Resolver el problema 4 para una lente divergente. Resp. 0.64, 0.4, 0.25.

 

4. RESOLUCIÓN

La resolución óptica o el poder de resolución se refiere a la capacidad del telescopio de mostrarnos una imagen nítida cuando se observan dos objetos muy cercanos. Por ejemplo, si de noche vemos un automovil a lo lejos, veríamos que sus luces frontales forman una sola fuente de luz y pensaríamos que es mas bien una motocicleta. Solo a medida que se acerca, podremos distinguir dos fuentes de luz y que se trata de un automovil. Lo mismo sucede con las estrellas, especialmente, con aquellas que estan muy cerca entre sí. Si nuestro telescopio no tiene una buena resolución , veremos a las dos estrellas como una sola.

Entonces, a la hora de adquirir un telescopio, lo que queremos es que tenga un poder de resolución aceptable. Para lograr esto, se incrementa la abertura de la lente. En astronomía, es importante tener imagenes de alta resolución para estudiar los detalles, por ejemplo, de la superficie de un planeta, o los detalles de una galaxia distante, o como se había mencionado antes, distinguir entre una estrella simple de un sistema binario de estrellas.

La resolución de un telescopio se puede calcular utilizando una expresion matemática que proviene de una aproximación en lo que se llaman las "funciones de Bessel" del criterio de Rayleigh. Este criterio especifica la mínima separación entre dos fuentes de luz. En óptica, las fuentes de luz que atraviesan una lente circular, estan limitadas por la difracción de la luz. La difracción se caracteriza por un patrón de regiones claras y oscuras. La parte clara y central de este patron se denomina "disco de Airy", cuyo diametro está relacionado con la longitud de onda de la luz λ y el diametro de la abertura de la lente D. Esta separación angular o poder de resolución está definida así,

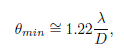
De esta manera, observamos que a mayor diametro, menor el ángulo, lo que implica una mejor resolución . Por otro lado, si la longitud de onda es corta como el azul, entonces tenemos mejor resolución .

El poder de resolución se mide en radianes. A continuación , algunas conversiones:

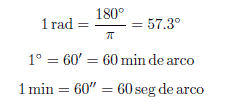
Ejemplo 6. El Gran Telescopio Canaris de 10.4 m de diametro, opera en longitudes de onda ópticas (0.00006 cm). ¿Cual es la máxima resolución en microradianes y en milisegundos de arco?

Solución. Necesitamos que las unidades de medida sean las mismas. Así que el diametro es D = 10.4 m = 1040 cm. Mediante la ecuación para la resolución , hallamos

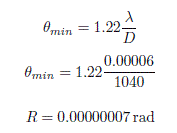
Multiplicamos (x10⁶) para que este en microrads:

Multiplicando R en rads por

obtenemos el resultado en:

Ejemplo 7. Para una longitud de onda en el visible de λ = 530 nm, compare la resolución de un par de binoculares (D = 50 mm) y de un telescopio pequeno (D = 200 mm). Los resultados expreselos en segundos de arco.

Solución. Vamos a uniformizar las unidades a mm. Entonces, la longitud de onda en el visible es λ = 530 x 10^-6 mm. El poder de resolución de los binoculares es R = 2.7 segundos de arco. Para el telescopio pequeno de D = 200 mm de diametro, su resolución es de R = 0.67 segundos de arco. Se nota que el telescopio de mayor abertura ofrece mejor resolución .

Ejemplo 8. El telescopio espacial Hubble tiene un diametro de 2.4 m. Para la misma longitud de onda del ejemplo anterior, ¿cual es su máxima resolución?

Solución. Datos: D = 2400 mm. Asi, la resolución del telescopio espacial Hubble es R = 0.06 segundos de arco.

Problema 6. Un astronomo quiere diseñar un sistema que le permitira estudiar los cráteres en la Luna que tienen alrededor de 0.1 segundos de arco de diametro vistos desde la Tierra. ¿Cuál es el tamaño minimo de la abertura que necesita para realizar su estudio, si la longitud de onda es 535 nm? Resp. 1346 mm

Problema 7. Una astronoma quiere diseñar un telescopio infrarrojo con una resolución de 1 segundo de arco para una longitud de onda de 20 /xm. ¿Cual debería ser el diametro del espejo? Resp. 5.1 m

 

5. GANANCIA DE LUZ Y AUMENTO

Un telescopio suele estar equipado con un juego de lentes de aumento. Con estas lentes, el telescopio tiene mayor potencia, es decir, que nos acerca mas al objeto. Por ejemplo, si queremos ver un objeto que est a 100 m como si estuviera a 10 m, utilizaríamos la lente de 10x de aumento. Lo que se hace es dividir la distancia del objeto entre el aumento de la lente (100/10). El aumento es el incremento aparente del tamaño angular. Está dado por

ecuación que habíamos visto anteriormente en la Sec. 3.

Por otra parte, una característica del telescopio es la ganacia de luz. La ecuación de la ganancia de luz esta dada por:

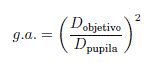
Por ejemplo, un telescopio con 70 mm de abertura sobre la abertura del ojo humano de mas o menos 7 mm, ofrece una ganancia de 100. Esto permitiría observar estrellas que se ven muy tenues a simple vista. Evidentemente, existen otros factores que afectan a esta ganancia como los efectos de reflexion, de dispersion y de absorción de la luz. Además de la longitud de onda de la luz incidente. Normalmente, los telecopios tienen una transmision de luz del 80%.

 

6. GALILEO

Galileo Galilei fue el primer cientifico italiano que desarrollo las bases del abordaje científico que se utiliza en cualquier proyecto de investigación actual. Mediante los experimentos que realizo y la aplicación de la matemática, estudió las leyes del movimiento y realizo varios descubrimientos que pusieron en duda el dogma impuesto sobre la geocentricidad.

Galileo nacio un 15 de febrero de 1564, en Pisa, Italia. Su padre, Vincenzo Galilei, fue musico y obligó a su hijo a estudiar medicina. Si bien Galileo, en realidad, quería ser sacerdote, ingreso a la Universidad de Pisa, en 1581, para estudiar medicina y matematicas. Después de cuatro años de estudio en la universidad, Galileo, a sus 21 años, dejó la universidad y trabajo dando clases de matemática, de manera particular primero, y luego en la Universidad de Pisa. Cuando su padre fallecio, en 1591, Galileo se convirtio en el principal proveedor de la familia.

Debido a su innata curiosidad como cientifico, realizo estudios sobre la balanza hidrostática, los planos inclinados, la caida libre, el movimiento parabolico y el péndulo para medir incrementos de tiempo. En 1609, Galileo se entero de la invención de un instrumento que permitía observar objetos lejanos y en el transcurso de un mes, lo convirtio en un instrumento para observar los cielos. De esa manera, Galileo observo que Júpiter tenía lunas que giraban a su alrededor, que la Luna tenía montañas, que el Sol presentaba manchas y que Venus tenía fases como nuestra Luna. Incluso, observo que Saturno parecia ser un planeta con "orejas".

1609 es el año en que Galileo revolucionó la astronomia, abriendo una nueva ventana hacia el estudio del Universo, mediante "dos pedacitos de vidrio" ajustados en un tubo. Posteriormente, el telescopio fue evolucionando. Al darle mayor longitud se obtenían mejores imagenes. Por ejemplo, Saturno ya no era un planeta con orejas, sino un planeta con anillos. Todas las observaciones iniciales de Galileo, sirvieron de sustento para el modelo heliocentrico, ganandose enemistades en la Iglesia y finalmente, siendo víctima de las injusticias de los prejuicios santificados. Murio bajo arresto domiciliario en 1642, en Toscana.

Todos los estudios de Galileo, su producción bibliográfica y su actitud como científico son dignos de admiración . No por nada, es denominado como el "padre" del metodo científico.

 

7. CUESTIONARIO

1. ¿Cuales son los principales tipos de telescopio?

El refractor, el reflector, y el catadioptrico.

2. ¿Cuál es la diferencia entre reflexión y refracción ?

En la reflexion, el haz de luz incidente sobre una superficie es reflejado, como en un espejo.

En la refracción , el haz de luz pasa de un medio a otro sufriendo una desviación , como un lápiz que se ve aparentemente "torcido" en un vaso con agua.

3. ¿En que se diferencia un telescopio refractor y reflector?

El telescopio refractor utiliza lentes, normalmente es largo y sirve para realizar observaciones terrestres, planetas, la Luna y algunas estrellas binarias.

El reflector utiliza espejos, es mas compacto y sirve

para observar objetos de poca intensidad como galaxias, nebulosas y cumulos estelares.

4. ¿En que consiste el aumento en un telescopio?

El aumento del telescopio es una razon entre la altura de la imagen y la altura del objeto, o la razon entre la longitud focal de la imagen y la longitud focal del objeto. La lentes adicionales que tiene un telescopio se caracterizan por su aumento, que esta representado, por ejemplo, por 10x. Esto significa que si el objeto est a 100 m y utilizamos esta lente, observaríamos al objeto como si estuviera a 10 m.

5. ¿Qué es la resolución de un telescopio?

Es la capacidad de distinguir dos objetos muy cercanos. Si el telescopio no tiene un poder de resolución aceptable y apuntamos hacia una estrella binaria, la veríamos como una sola. Incrementando el poder de resolución podemos distinguir los detalles del objeto.

 

8. CONCLUSIONES

El telescopio permite observar los objetos celestes gracias a las leyes basicas de óptica. En esta rama de la fisica, se estudian las características de lentes y espejos. Las lentes refractan la luz así como un prisma lo hace y los espejos reflejan las imagenes. Dependiendo de la forma de las lentes y los espejos, las imagenes pueden aumentar de tamaño, reducirse, invertirse o formarse en el infinito.

En un telescopio, las dos lentes se situan de modo que se forma una imagen real e invertida cerca del punto focal del ocular. Las dos lentes, que normalmente son biconvexas, estan separados por una distancia ƒ_obj + ƒ _ocular que corresponde a la longitud del tubo del telescopio. Luego, el ocular forma una imagen invertida y mas grande que la primera imagen.

El aumento tiene importancia para observar objetos como el Sol, la Luna o planetas, pero las estrellas lejanas seguiran viéndose como simples puntos de luz. A menos que se construyan telescopios de gran abertura que permitan el ingreso de una mayor cantidad de luz. La desventaja es que construir espejos o lentes de diametros grandes es muy costoso y complicado. Por lo tanto, la elección de un telescopio depende de lo que se quiere observar y el presupuesto con el que se cuenta.

Desde las observaciones de astronomos aficionados hasta las obtenidas por los grandes telescopios del mundo, todas han resultado de estos conceptos de óptica. La necesidad de conocer aún más el Universo ha llevado incluso a posicionar telescopios fuera de la Tierra, como el Hubble, que en 1995 obtuvo por vez primera la imagen de un Universo joven de hace 13000 millones de años.

Nuestra fascinación por los cielos y nuestra curiosidad nos llevar a desarrollar la tecnología necesaria para colmar nuestras inquietudes sobre el Universo en el que vivimos. Es solamente cuestion de tiempo.

El contenido de esta revision bibliográfica ha sido obtenida de las referencias que se citan a continuación . Se pueden revisar las paginas web: Gil (2016), Navarro (2016),Exploratorium (2018), Science Facts (2018), Hernaez (2017), Berner (2015), School bag (2014), American Association of Physics Teachers (2012), Terratec S.R.L. (2018),Spacemath NASA: Equation (2018), Spacemath NASA: Resolution (2018), TelescopeOptics: Resolution (2018), TelescopeOptics: Functions (2018), Nagler (2018), PBS & WGBH Educational Foundation (2018).Si desea un estudio mas formal de la óptica referirse a Young & Freedman (2009), Serway (1997), Resnick (1994), Beltran & Braun (1977).

Un excelente complemento conceptual es Hewitt (2007) y las guías de astronomía: Ridpath (2007), Atlas de Astronomía (1994).

 

AGRADECIMIENTOS

Agradezco a Dr. Martín Subieta, Lic. Gonzalo Pereira, Daniela Ochoa, Dr. Santiago Conde, Lic. Rubber Muñóz y al Dr. Diego Sanjinés por la revisión detallada y las pertinentes observaciones para mejorar el texto.

Ademas, reconocer la colaboración y el auspicio de la empresa Terratec S.R.L.: Astronomía y Ciencia Experimental para concretar este proyecto.

 

REFERENCIAS

Gil Andani, I. (2016), Astronomylab. http://www.astronomylab.net.         [ Links ]

Navarro Díaz, I. (2016), Tipos de telescopios, accesorios ópticos e instrumentación, https://neudron.blogspot.com.         [ Links ]

Exploratorium. (2018), Science Snacks. https://www.exploratorium.edu.         [ Links ]

Science Facts. (2018), Diverging Lens. https://www.sciencefacts.net.         [ Links ]

Hernaez, S. (2017), Cómo funciona un telescopio. https://www.aboutespa~nol.com.         [ Links ]

Berner, B. (2015), The Laboratory for Research on the Structure of Matter. It's all smoke and mirrors: The Physics of Images. https://www.lrsm.upenn.edu.         [ Links ]

School Bag. Ministry of Education, Singapore. (2014),Magic or Science? The classroom comes alive!. https://www.schoolbag.sg.         [ Links ]

American Association of Physics Teachers. (2012), High School Photo Contest Top 100 Gallery. https://www.aapt.org.         [ Links ]

Terratec S.R.L. (2018), Astronomía y Cs. Experimental. http://www.terratec.com.bo.         [ Links ]

Spacemath NASA (2018), The most important equation in astronomy. http://www.spacemath.gsfc.nasa.gov.        [ Links ]

Spacemath NASA (2018), Telescope Resolution. http://www.spacemath.gsfc.nasa.gov.        [ Links ]

TelescopeOptics.net (2018), Telescope Resolution. www.telescope-optics.net.        [ Links ]

TelescopeOptics.net (2018), Telescope Functions. www.telescope-optics.net.        [ Links ]

Nagler, A. (2018), How to choose your telescope magnification. www.skyandtelescope.com.        [ Links ]

PBS & WGBH Educational Foundation. (2018), Galileo: Timeline ofhis life. www.pbslearningmedia.org.        [ Links ]

Young, H. D. & Freedman R. A. (2009), Física Universitaria, con física moderna 2, Peason Educación .

Serway, R. A. (1997), Física Tomo II, McGraw-Hill Interamerican Editores, S.A. de C.V.        [ Links ]

Resnick, R. Halliday, D. Kenneth, S. K. (1994), Física Vol 2, Compañía Editorial Continental, S.A. de C.V.        [ Links ]

Beltran, V. & Braun, E. (1977), Principios de Física Curso de Introducción , Editorial Trillas.

Hewitt, P. G. (2007), Física Conceptual, Pearson Educación .

Ridpath, I. (2007), Guía Ilustrada: Astronomía, Jorge Zahar Editor Ltda.        [ Links ]

V. V. A. A. (1994), Atlas de Astronomía: Descubrir el Universo, Cultural S.A. de Ediciones.        [ Links ]